1. High velocity impact performance of three-dimensional woven composites
三维机织复合材料的高速冲击性能研究
翻译:张寅枭
基于波的传播和弹丸与目标之间的能量平衡,建立了理论预测模型,来研究三维机织复合材料在高速冲击下的性能。从弹体接触靶板开始,按照选定的时间步长迭代计算不同时刻弹体运动状态与靶板应力应变分布,并判断当前与弹体接触的位置是否发生失效,该模型考虑了剪切冲塞与基体开裂两种失效模式。在各时间段计算靶板吸收的能量,包括应变能与摩擦热。根据应力波扫略的区域,计算靶板产生的应变能。包括主纤维束内由于应力波传递产生的应变能,以及受到牵引的次要纤维束的应变能。通过将多个算例的理论预测结果与试验结果对比,证明了该模型能较为准确地预测三维机织复合材料的冲击力学性能。该文预测结果表明,在三维机织复合材料受冲击过程中,剪切冲塞、摩擦热为主要的能量吸收机制(如图1)。
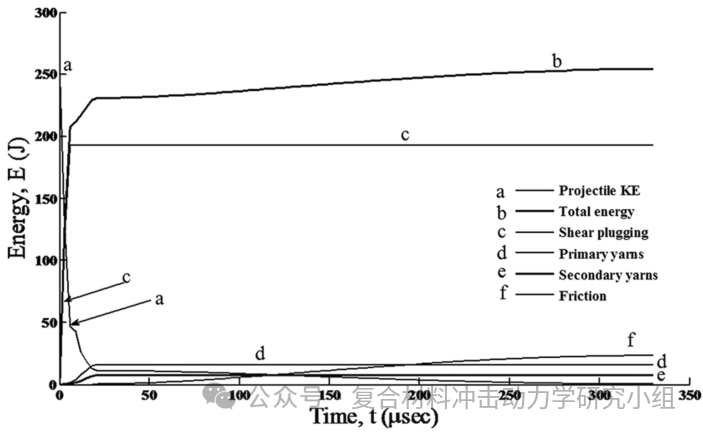
图1. 冲击过程中能量吸收示意图。
Pavani U, C V S Kumar, & Nithin S N, et al. High velocity impact performance of three-dimensional woven composites. J Strain Anal Eng. 47(2012): 419-431.
2. Influence of reversible swelling and preload force on the failure behavior of a lithium-ion pouch cell tested under realistic boundary conditions
可逆膨胀和预紧力对实际边界条件下测试锂离子软包电池失效行为的影响
翻译:陈子烨
本文研究了在实际边界条件下,预紧力和可逆膨胀对锂离子软包电池的失效行为的影响。研究通过对36个软包电池在不同边界条件下进行平端圆柱挤压测试,直至发生机械故障和热失控,来探讨这些因素对电池性能的影响。在实验中,电池在30%的充电状态(SOC)下分别施加0、300和4000牛顿的预紧力,并在挤压前充放电至0%、30%、60%或100% SOC。
研究发现,最大压痕力、初始刚度和故障行为均与预紧力有关。隔膜内部应力随预紧力增加而导致更早的短路和机械故障,尤其是在较高的预紧力下更为显著。此外,机械约束在热失控过程中导致气体压力增加。这些发现对于电池模块中软包电池的安全性测试和仿真具有重要意义。总而言之,这项研究为理解软包电池在实际应用中的机械滥用和热失控行为提供了新的建议,有助于改善电池设计和安全性能。
(a)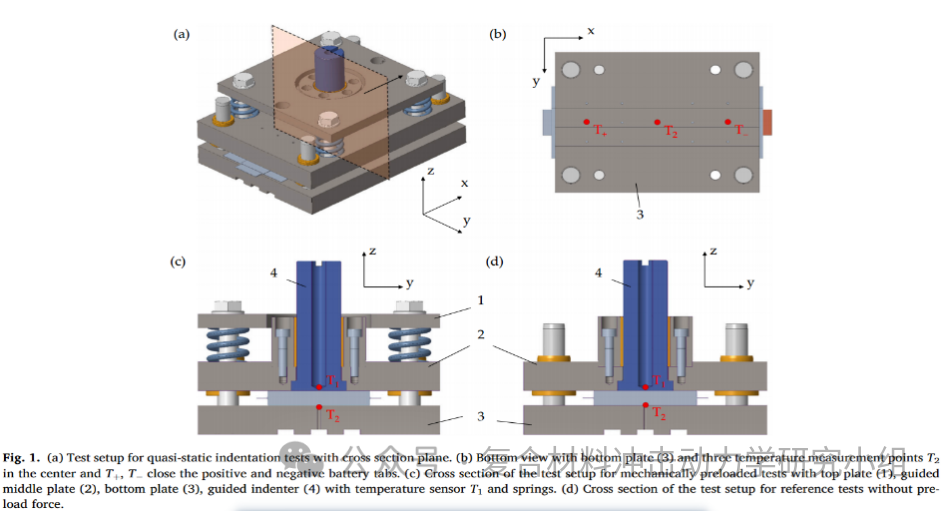
(b)
图2. (a) 测试装置图;(b)实际结构与电池压痕图。
Höschele P, Heindl S F, Erker S, et al. Influence of reversible swelling and preload force on the failure behavior of a lithium-ion pouch cell tested under realistic boundary conditions[J]. Journal of Energy Storage, 2023, 65: 107228.
3.Determination of material parameters in constitutive models using adaptive neural network machine learning
自适应神经网络确定本构模型材料参数
翻译:李子琪
对于具有时间依赖性的非线性本构建模,一个挑战是识别潜在的大量材料参数。此文提出了一种基于奇异值分解( Singular Value Decomposition, SVD)和自适应神经网络(neural network, NN)来确定这些参数的有效方法。对于时间相关应力序列,SVD压缩数据并为神经网络提供输出。训练神经网络,建立材料参数到SDV降维后应力的映射关系。训练后的网络可以快速计算大量材料参数下的材料响应。然后将这些响应与实验数据进行比较,以确定最佳参数。由于对于不同的本构模型,需要不同的隐藏层数和训练集大小来实现最佳预测,因此,文中设计了一种自适应网络来自动更新神经网络和训练集,以实现任何本构模型的材料参数确定。文中对三种具有不同时间依赖性行为的大变形水凝胶(本构模型分别有4、9和13个材料参数)进行单轴循环和松弛测试来进行验证。结果表明,所提出的方法可以很好地预测不在训练集中的应力历史,并且能够适应各种各样的本构模型,显示出该方法的通用性和可扩展性。
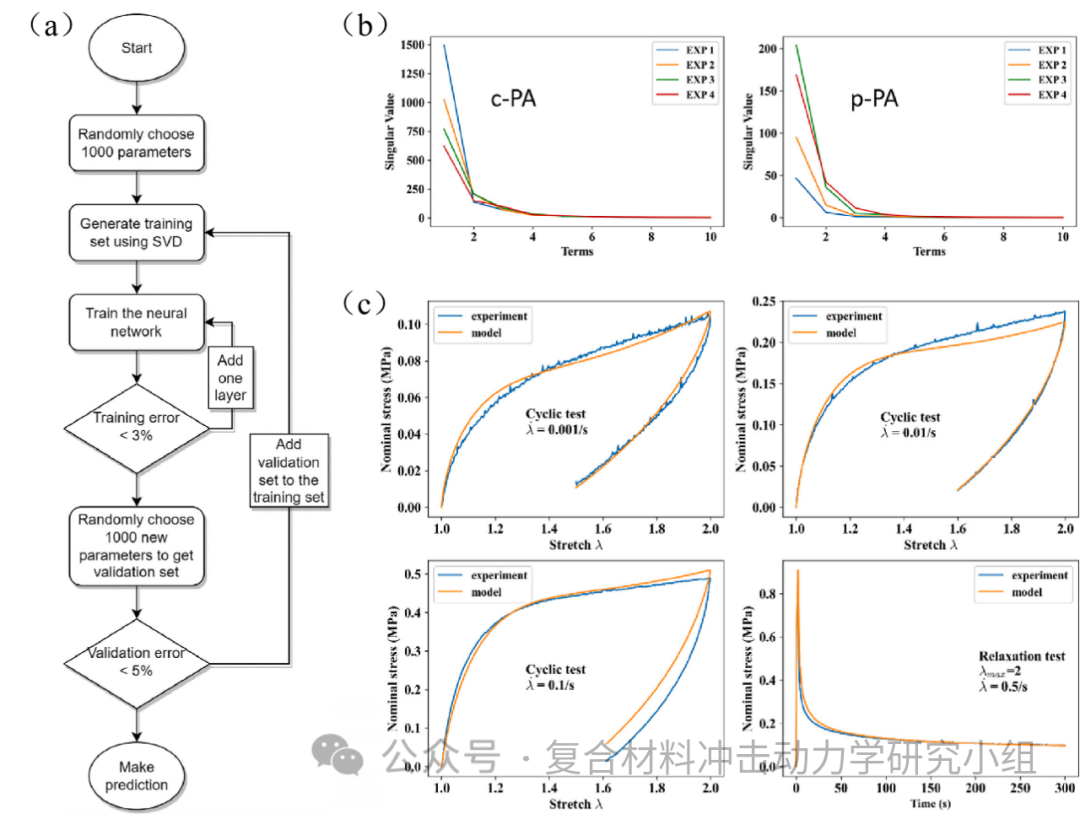
图3. (a)自适应神经网络工作流程;(b)能够反映不同模型和加载历史的SDV奇异值;
(c)最佳材料参数下,神经网络输出应力与不同拉伸率下循环和松弛试验数据的对比。
J. Wang, B. Zhu, C.-Y. Hui, A.T. Zehnder, Determination of material parameters in constitutive models using adaptive neural network machine learning, Journal of the Mechanics and Physics of Solids 177 (2023) 105324.
4. Ceramizable phenolic adhesive modified by different inorganic particles: A comparative study of thermal stability, bonding strength and bonding mechanism
不同无机颗粒改性酚醛陶瓷胶粘剂的热稳定性、粘接强度和粘接机理的比较研究
以ZrSi2颗粒或ZrSi2/B4C混合颗粒为无机填料,制备了两种可陶瓷化的酚醛树脂胶粘剂。通过热重分析、Al2O3接头剪切强度、扫描电镜、能谱仪、X射线衍射仪和X射线光电子能谱仪对胶粘剂的热稳定性、结合强度、微观结构和相组成进行了研究。结果表明,这两种胶粘剂在600℃以下的粘合机理基本相同:随着酚醛树脂的热解,微观结构出现缺陷,而填料没有显著变化,因此在600℃时的粘接性能降至最低。600℃以上两者具有不同的粘接性能和陶瓷化演变规律:由于添加了第二相粒子B4C,ZrSi2/B4C改性酚醛胶粘剂在1200℃处理后的结合强度可达36.6MPa,而ZrSi2改性酚醛胶在相同条件下的结合强度仅为17.5MPa。主要原因是添加的B4C在ZrSi2之前发生氧化反应,氧化产物B2O3液相不仅与ZrSi2反应形成抗氧化的ZrB2,而且可以溶解粘合剂的高温缺陷,并在高温下与Al2O3衬底化学结合。
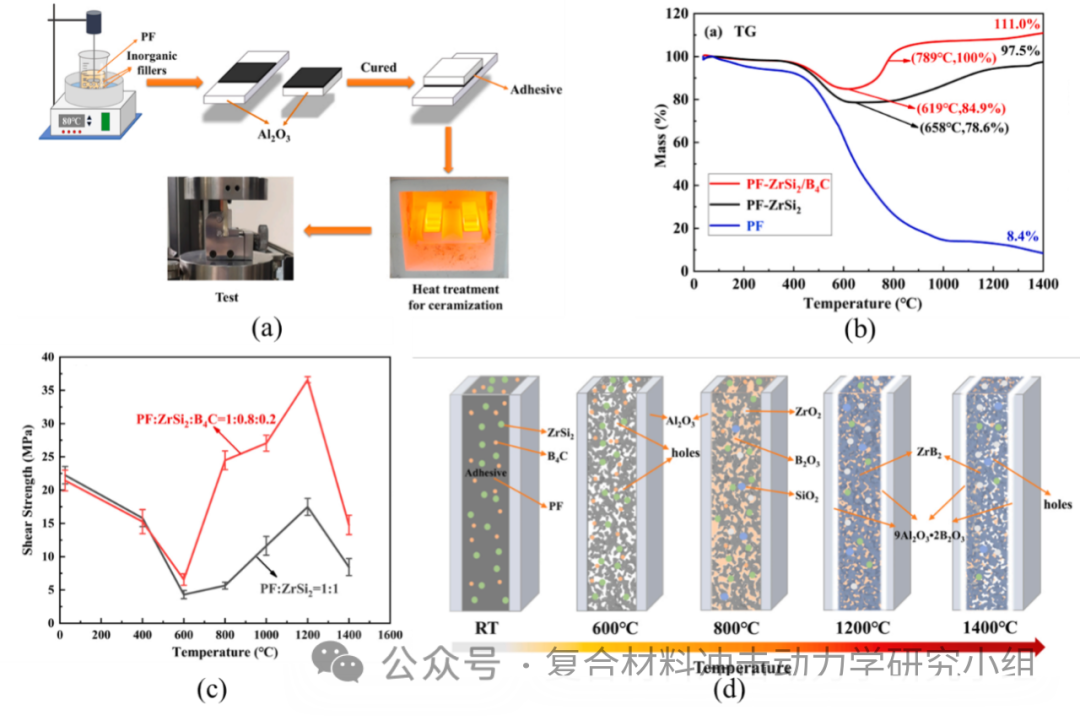
图4. (a)材料制备以及测试过程;(b)热失重实验结果;(c)不同温度下的粘接性能测试结果;(d)不同温度下的材料体系陶瓷化示意图。
Cunku Wang, Jie Ding, Zhixiong Huang, Yingluo Zhuang, Yan Li, Minxian Shi, Yan Qin. Ceramizable phenolic adhesive modified by different inorganic particles: A comparative study of thermal stability, bonding strength and bonding mechanism. Journal of the European Ceramic Society, 2023, 43:64–72.
5. Machine learning-based constitutive model for J2- plasticity
基于机器学习的J2塑性本构模型
机器学习技术已广泛用于预测不同结构和材料体系的力学行为。该文在各向同性硬化和相关流动规则的框架中,采用了人工神经网络(ANN)模型来取代经典理论本构模型中的非线性应力积分方案,提出了一种基于机器学习的J2塑性模型(图5.(a))。该模型的训练集是基于单单元数值模型,通过主应力空间中经典的返回映射方法生成的。模型训练结束后,该模型以UMAT用户子程序的方式实现了数值植入。该文首先开展了单单元模型和狗骨状拉伸试样(图5.(b))的数值仿真工作,用于验证模型的准确性。随后,该文开展了圆杯拉伸数值仿真工作(图5.(c)),用于验证模型在预测完全非线性路径下力学行为的有效性,并将经典的J2塑性模型的仿真结果作为参考结果。研究结果表明,基于机器学习的J2本构模型在保证计算结果精度的同时,也体现出计算效率上的优势。该文研究成果显示了以机器学习技术为代表的新型解决方案在计算力学领域的应用潜力。
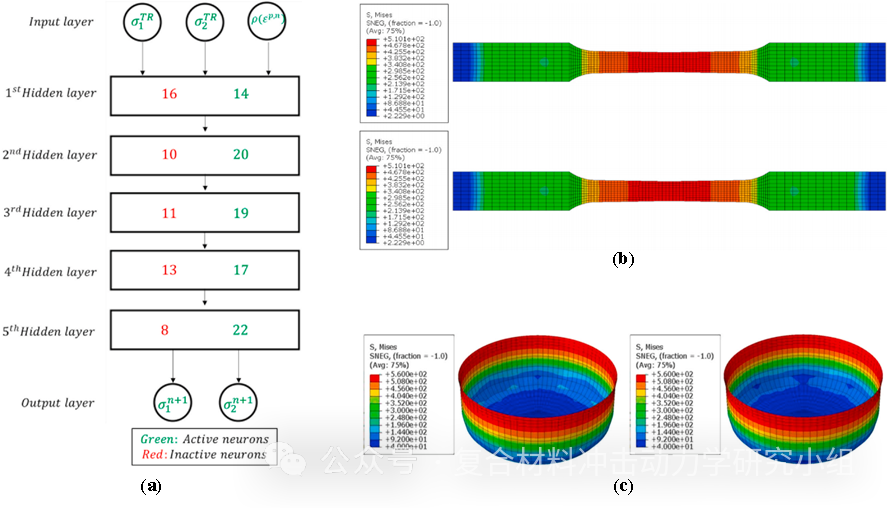
图5. (a)基于ANN模型的J2塑性模型;(b)狗骨状拉伸试样的数值模拟;(c)圆杯拉伸模拟。
Jang D P, Fazily P, Yonn J W. Machine learning-based constitutive model for J2- plasticity. Int J plasticity 2021; 138. 102919.
6. Mechanical properties prediction of composite laminate with FEA and machine learning coupled method
用有限元分析和机器学习耦合的方法预测复合材料层合板的力学性能
为了预测复合材料层合板的力学性能,建立了一种耦合有限元分析和机器学习的方法,对随机应力状态下Puck理论的失效因子、开孔层合板的失效因子和临界屈曲特征值进行了分析,为提高计算效率、降低复合材料的设计成本和更有效地构建复合材料的数字化强度系统提供了一种新的数据驱动框架。通过编写Abaqus脚本,建立了复合材料层合板的参数化有限元模型,并生成了大量虚拟样本,其中80 %为训练样本,20%作为测试样本。建立了人工神经网络(ANN)模型和随机森林(RF)模型对这些样本进行训练和测试,以预测相应参数的力学性能。通过对这些力学参数的预测结果和有限元结果进行分析,ANN和RF模型的预测结果与有限元分析值的曲线吻合良好,计算得到的均方根误差较小。结果表明,将有限元分析软件与机器学习模型耦合的方法可以有效地预测复合材料层合板的力学性能。此外,ANN模型的准确率和预测效率高于RF模型,RF模型的学习过程比ANN模型的学习过程花费更少的时间,可以根据精度和计算成本等需求选择ANN或RF模型。
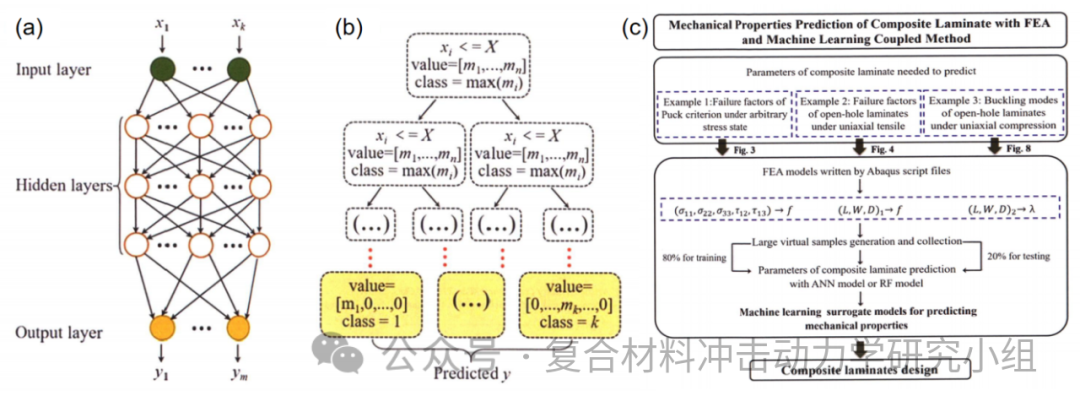
图6. (a)人工神经网络模型的结构;(b)RF模型的决策树流程图;(c)耦合有限元分析和机器学习预测复合材料层合板力学性能的流程图。
Zhang C, Li Y, Jiang B, et al. Mechanical properties prediction of composite laminate with FEA and machine learning coupled method[J]. Composite Structures, 2022, 299: 116086.
7. Flat glass fibres: The influence of fibre cross section shape on composite micromechanics and composite strength
平板玻璃纤维:纤维截面形状对复合材料微观力学和复合材料强度的影响
翻译:南天
许多用于复合增强的纤维都具有非圆形横截面,最近非圆形截面玻璃纤维产品已上市。本文探讨了这种非圆形截面纤维对纤维-基体界面应力传递的微观力学以及由此产生的复合材料强度性能变化的潜在影响。分析模型显示:与具有相同横截面积的圆形纤维相比,具有非圆形纤维的复合材料的临界纤维长度总是更小。这可能导致非连续纤维增强复合材料的强度性能发生重大变化。此外,研究表明,纤维横截面的非圆度对使用单纤维微观力学测试表征界面强度具有重要影响。
(a)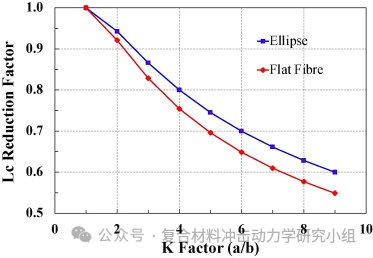
(b)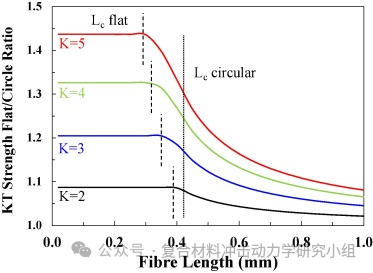
图7. (a)扁平纤维和椭圆纤维的Lc折减系数(C)与扁平度(K)的关系;(b)Kelly-Tyson方程预测了不同平整度比(K)纤维单向不连续GF-PA复合材料的扁平/圆强度贡献比。
James L. Thomason, Flat glass fibres: The influence of fibre cross section shape on composite micromechanics and composite strength, Composites Part A: Applied Science and Manufacturing, Volume 169, 2023, 107503, ISSN 1359-835X
8. Geometrically nonlinear dynamic analysis of laminated composite plate using a nonpolynomial shear deformation theory
基于非多项式剪切变形理论的复合材料层合板几何非线性动力分析
为设计承受动态载荷的复合材料结构,需要建立一个涉及较高应变率下和不同机制的本构模型,以便于预测材料的损伤和失效。该文提出了一个包括粘弹性、粘塑性、纤维旋转和损伤的综合模型,以尽可能表征纤维增强复合材料动态加载过程中的各种响应。选择LaRC失效准则,并引入损伤参数d1、d2和d6分别代表纤维、基体和剪切中的损伤。材料在达到任意失效模式后,触发相应的损伤参数。基于Maimi连续体损伤模型计算损伤的开始和演变,并通过相关损伤参数应用于薄板的刚度退化。在加载过程中,纤维可以旋转,并根据连续介质力学将初始材料方向从薄层指向改变为真实材料方向。此外,采用三维正交各向异性粘塑性模型对该材料的粘弹-粘塑性行为进行建模,并根据应变率的动态值更新材料的弹性性能和最终强度,进而更新动态载荷下的损伤刚度。而实际上,动态刚度则是准静态刚度的函数。该模型能较好地反映应变率对材料性能的影响,并能较好地预测复合材料层合板在中、高应变率下的响应和最终强度。
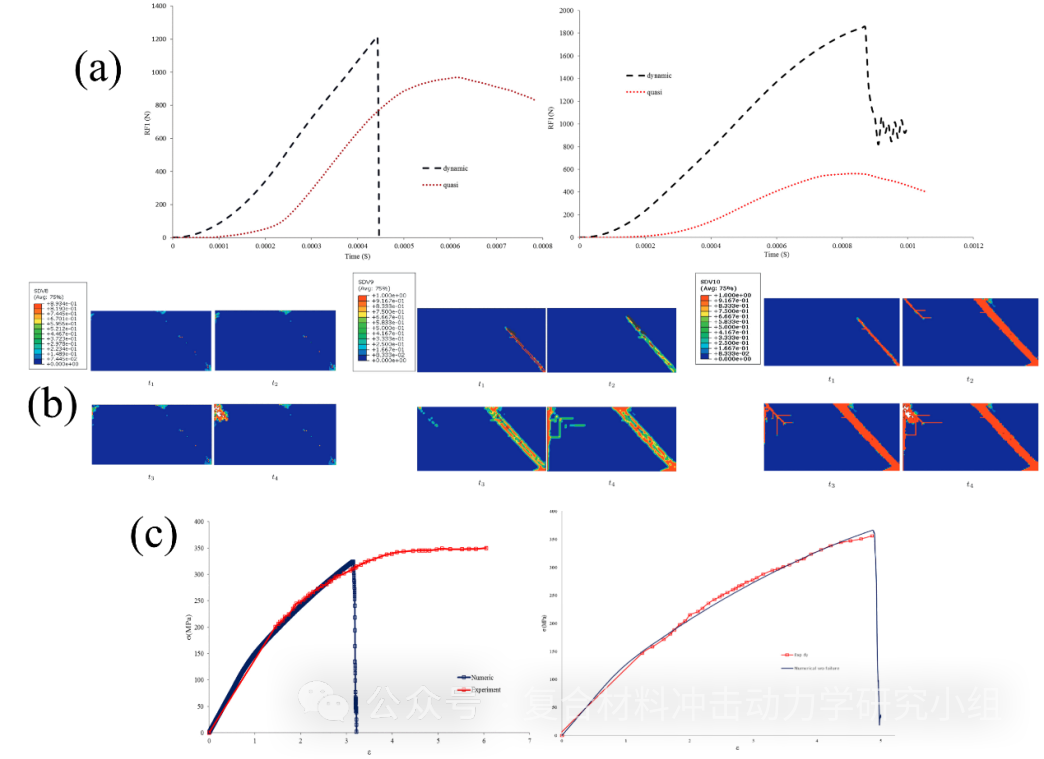
图8. (a)15°和30°层合板在准静态和动态下反作用力随时间的曲线;(b)30°模型中d1、d2和d6损伤参数的演变;(c)45°和60°层合板动态条件下的应力-应变曲线比较。
Eskandari S, Andrade Pires F M, Camanho P P, et al. Analyzing the failure and damage of FRP composite laminates under high strain rates considering visco-plasticity[J]. Engineering Failure Analysis, 2019, 101: 257-273.

